Concrete Cellular Automata

Definition: the local rule $f$ is such that $f(x_1,\ldots,x_k)\in\{x_1,\ldots,x_k\}$
ACML command lines:
acml random --- captive true dimension 1 states 6 radius 2
acml random --- captive true dimension 2 states 4 neighborhood vonNeumann
Related papers:
- G. Theyssier, Captive Cellular Automata
- G. Theyssier, How Common can be Universality in Cellular Auomata?

Definition: the local rule $f$ is such that $f(x_1,\ldots,x_k)=f(x_{\pi(1)},\ldots,x_{\pi(k)})$ for any permutation $\pi$
Said differently, the local rule only depends on the multiset of states in the neighborhood
For two states, multiset CAs correspond exactly to the so-called 'totalistic CAs'. For three or more states, totalistic CAs are strictly included in multiset CAs.
ACML command lines:
acml multiset --- captive false dimension 1 states 4
acml multiset --- captive true outer true dimension 2 states 4 radius 1
Related paper:
- L. Boyer, G. Theyssier, On Local Symmetries and Universality in Cellular Automata

Definition: the local rule $f$ is such that $f(x_1,\ldots,x_k)=f(y_1,\ldots,y_k)$ whenever $\{x_1,\ldots,x_k\}=\{y_1,\ldots,y_k\}$
Said differently, the local rule only depends on the set of states in the neighborhood
ACML command lines:
acml set --- captive true dimension 2 states 7 neighborhood vonNeumann
acml set --- captive false dimension 1 states 6 neighborhood vonNeumann
Related paper:
- L. Boyer, G. Theyssier, On Local Symmetries and Universality in Cellular Automata

Definition: the local rule $f$ is such that $f(x_1,\ldots,x_k)=\pi^{-1}\circ f\bigl(\pi(x_1),\ldots,\pi(x_k)\bigr)$ for any permutation of states $\pi$
Said differently, the local rule is blind to colors and only depends on equality/non-equality verified between states in the neighborhood
They are always "almost captive" and "almost always" captive. More precisely, the only transitions than can possibly violate the captive condition are those where exactly $n-1$ different states appear in the neighborhood ($n$ being the total number of states).
ACML command lines:
acml colorblind --- dimension 2 states 6 neighborhood vonNeumann
acml colorblind --- dimension 1 states 4 radius 3
Related paper:
- V. Salo, I. Törmä, Color Blind Cellular Automata

Definition: the CA has sate set $\{0,\ldots,n-1\}$ and is such that a cell in state $q$ can only update to state $q+k \bmod n$ or stay unchanged
The original and well-known family of cyclic CAs by Fisch-Gravner-Griffeath essentially consists in choosing $k=1$ and adding a captive condition to the definition above: the cell update only happens when state $q+k\bmod n$ is present in the neighborhood. This can be further parametrized by requiring the number of occurrences of state $q+k\bmod n$ to be above some threshold.
ACML command lines:
acml "random cyclic" --- dimension 1 states 4 radius 4 threshold 1 multiset false instability 0.45
acml "random cyclic" --- dimension 1 states 5 radius 1 threshold 0 multiset true instability 0.5
acml "random cyclic" --- dimension 2 states 5 radius 1 threshold 1 multiset true instability 0.75 neighborhood vonNeumann
acml "random cyclic" --- dimension 2 states 5 radius 1 threshold 2 multiset true instability 0.7 neighborhood Moore "forward jump" 2
Related papers:
- R. Fisch, J. Gravner, D. Griffeath , Cyclic Cellular Automata in Two Dimensions
- R. Fisch, The one-dimensional cyclic cellular automaton: A system with deterministic dynamics that emulates an interacting particle system with stochastic dynamics
- B. Hellouin de Menibus, M. Sablik , Self-organization in Cellular Automata: A Particle-Based Approach

2 states von Neumann neighborhood
To my knowledge, no smaller 2D intrinsically universal CA is known
ACML command line:
acml "fun me howmany -> if howmany 1 = 3 then 1-me else if me = 0 && howmany 1 = 4 then 1 else me" --- states 2 dimension 2 neighborhood vonNeumann
Related papers:
- E. R. Banks, Universality in Cellular Automata
- N. Ollinger, Universalities in Cellular Automata: a (short) survey

next-neighbors and 4 states
To my knowledge, no smaller 1D intrinsically universal CA is known
110 is known to be Turing-universal and P-complete but not known to be intrinsically universal
ACML source file: four_states.ml
Related papers:
- N. Ollinger, G. Richard, Four states are enough!
- M. Delorme and J. Mazoyer and N. Ollinger and G. Theyssier, Bulking II: Classifications of cellular automata

A 'proof-friendly' CA (introduced by J. Kari) solving the infinite firing squad problem
ACML source file: firing_squad.ml
Related papers:
- J. Kari, Rice's theorem for the limit sets of cellular automata
- P. Guillon, P.-E. Meunier, G. Theyssier, Clandestine Simulations in Cellular Automata

The Collatz function $$f:n\mapsto\begin{cases}n/2&\text{ if }n\text{ even}\\3n+1&\text{ if }n\text{ odd}\end{cases} $$ can be realized as one step of a CA that essentially multiplies by 3 in base 6
ACML source file: collatz.ml
Related paper:
- J. Kari, Cellular Automata, the Collatz Conjecture and Powers of 3/2

The maxiamal transient length of a nilpotent CA is not computable from the radius and the number of states.
Related paper:
- J. Kari, The nilpotency problem of one-dimensional cellular automata
My best finding for 1D 3-states next-neighbors is this one:
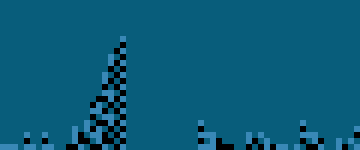
ACML command line:
acml number --- states 3 base 3 reverse true number 21100002001002012201010
My small collection of small nilpotent CAs

A linear CA over state set $\mathbb{Z}^d_{p^k}$ can be represented by a $d\times d$ matrix whose coefficient are Laurent Polynomials over $\mathbb{Z}_{p^k}$
ACML source file: linear.ml
Related papers:
- J. Kari, Linear Cellular Automata with Multiple State Variables
- J. Gütschow, V. Nesme, R. F. Werner, The fractal structure of cellular automata on abelian groups